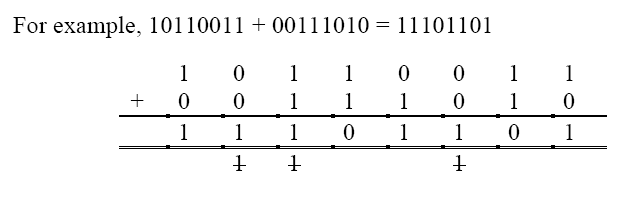
We can apply the normal rules of arithmetic to binary, just as we can to any other number system – and the only time this can get a little complicated is when considering binary subtraction – or negative binary since strictly the negative sign should not be used.
Negative Binary
To represent a binary number as being negative, we can use a system knows as “two’s compliment”. This can be thought of as like a car’s odometer, if the car drives a mile forwards, the odometer reads 000001, however, if it were to be forced back a mile, it would read 999999, which is like -1 mile. A negative binary number will always start with a 1 – this is known as the sign bit.
To convert a number to its two’s compliment, starting from the left we invert all the bits up to and not including the last 1. So, for example,
$$! =-( 00110011_2 )\\
= 11001101_2 $$
To convert a two’s compliment number back to denary, consider the place value of the first bit to no longer be 128, but negative 128. So in our above example:
$$!
=64+8+4+1-128\\
=-51
$$
Strictly speaking two’s compliment is calculated by inverting all the bits (which is known as one’s compliment) and then adding one to get two’s compliment. The trick of inverting all the numbers up until the final 1 is a good trick though. It is also worth noting that zero can only be expressed as a series of 0’s in two’s compliment, since it is 1111…111+1, which will result in 000…00 with an overflow – which is always ignored.
Binary Addition and Subtraction
Binary addition and subtraction are carried out using the basic premises that 0+0=0, 1+0 = 1 and 1+1 = 10 (or 0 carry 1). In practice this is carried out much as you may expect:
To do binary subtraction, we have to convert the number to be subtracted to its two’s compliment form, and then treat the operation as an addition. This may seem a little obscure, but the same thing is actually true in denary, for example: 5 – 3 = 5 + -3
Binary Multiplication
In binary multiplication, the least significant bit of the operand is placed in line with each “1” value in the operator, and these shifted operands are then added together. This is better explained in an example, where 11000 is the operand (the right-most zero bit is the least significant bit) and 11000 is the operator:
$$!
\begin{array}{r}
11000 \\
\underline { \times 00011} \\
11000 \\
\underline{\underline { + 110000}} \\
1001000 \\
\end{array}
$$
References:
- Janet Lavery – Durham University Computer Systems, Machine Architecture Lecture 6, 2007
- A2 Computing Revision – Paul Nicholls – http://resources.r9paul.org/ASA2/Computing/A2ComputingRevision.pdf