A set is a collection of distinct objects considered as a whole.
[Wikipedia – http://en.wikipedia.org/wiki/Set ]
A set can be thought of as a collection of objects – or elements – and these objects can be anything, data – numerical – or indeed other sets. Elements in a set are in no particular order, and elements in a set must by definition be unique.
Introducing Sets
We can use a system called set builder notation to describe a set:
![]()
For example, the following is a valid set notation for a set of the integer values from 1 to 9.
![]()
Subsets
A subset is one or more element selected from a set. For an element to be a member of a subset, it must also have been a member of the parent set.
If A and B are sets, then A will be a subset of B if every element of A is also an element of B (denoted as $ A \subseteq B $. Equivalently we can say that B is a superset of A, if B contains all the elements of A (denoted as $ B \supseteq A $).
![]()
Proper Subset
A proper subset is one or more (but not all of the distinct) elements selected from a set. If A and B are sets, then A will be a proper subset of B if every element of A is also an element of B, but also there is one or more elements in B which are not part of A. This is denoted as $A \subset B$. Equivalently, B is a proper superset of A if B contains all the elements of A and more – $B \supset A $
$
\forall _x \left( {x \in A \to x \in B} \right) \wedge \exists _x \left( {x \in B \wedge x \notin A} \right)
$
Cardinality
The cardinality of a set is how many members it contains, as shown in the examples below:
$
\left| \phi \right| = 0 \\
\left| {\left\{ {1,2,3,4} \right\}} \right| = 4 \\
\left| {\left\{ {\left\{ {1,2} \right\},\left\{ {3,5} \right\}} \right\}} \right| = 2
$
Powerset
The powerset of a set, $S$ is denoted as $\mathcal{P}(S)$ is a set of all the subsets of that set. This is best explained in the example shown below:
$
S=\left\{ x,y,z\right\}\\
\mathcal{P}(S)=\left\{ {\phi ,\left\{ x \right\},\left\{ y \right\},\left\{ z \right\},\left\{ {x,y} \right\},\left\{ {x,z} \right\},\left\{ {z,y} \right\},\left\{ {x,y,z} \right\}} \right\}
$
Where the set s has a cardinality of n, the powerset will have a cardinality: $\left|\mathcal{P}(S)\right|=2^n$
Truth Set
The truth set is the set of values for which a predicate logic statement holds true. For example, the truth set of $$ \left\{ x \in \mathbb{Z}^+ \left| x^2 < 4 \right. \right\} $$ is {1}.
Tuples
A tuple is a set of objects, but one in which the order of the elements is significant. For example, the set {1, 2, 3} is equal to the set {2, 1, 3} since the order of elements in a set is not important. In a tuple however, {1,2,3} would not equal {2, 1, 3}. In order for one tuple $$A$$ to be equal to another $$B$$ all of the elements of A $$a_i$$ where $$_i$$ is an index, must equal all the elements of B, $$b_i$$.
Set Operators
Cartesian Product
Where A and B are sets, the Cartesian product of the two sets is a set containing all possible pairings of elements from each of the two sets.
$$!
A = \left\{ {1,2} \right\} \\
B = \left\{ {a,b,c} \right\} \\
A \times B = \left\{ {\{ 1,a\} ,\{ 1,b\} ,\{ 1,c\} ,\{ 2,a\} ,\{ 2,b\} ,\{ 2,c\} } \right\}
$$
Union
The union of two sets, P and Q is a set containing all the unique items of P and Q.
$$ A \cup B = \left\{ x \left| x \in A \vee x \in B \right. \right\} $$
Intersection
The intersection of two sets, P and Q is a set containing all the elements which exist in both A and B.
$$! A \cap B = \left\{ x \left| x \in A \wedge x \in B \right. \right\} $$
Difference
The difference between two sets A and B is a set containing all the elements which exist only in A, not in B.
$$ A – B = A \backslash B = \left\{ x \left| x \in A \wedge \neg\left( x \in B \right) \right. \right\} $$
Complement
The complement of a set is a set of all the possible elements which are not contained within the set. So if the domain is $$ \mathbb{Z} $$ and we have a set $$P$$ with members in the domain, then $$\overline P = \mathbb{Z}-P$$
Venn Diagrams
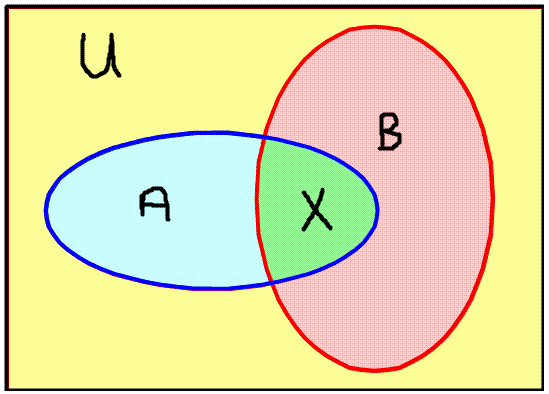
A Venn Diagram can be used to demonstrate sets and set operators. In the example below, A and B are sets are in domain of real numbers – $$ \mathbb{R} $$, and from the diagram there are a number of conclusions we can draw…
$$!
X=A \cap B \\
U= \mathbb{R} – \overline{A\cup B} \\
\left| A \cup B \right| = \left|A\right| + \left|B\right| – \left|A \cap B \right|
$$
Rules involving Sets
- De-Morgan’s theory applies to sets, this is discussed in more detail [Here]
- Order of processing operations is not important, $$\left( {A \cup B} \right) \cup C = A \cup \left( {B \cup C} \right) $$
- Identity Law: $$ A \cup \phi = A $$
References:
- Nick Holliman – Formal Aspects Set Theory – Lecture 3
- Nick Holliman – Formal Aspects Set Theory – Lecture 4
- Nick Holliman – Formal Aspects Set Theory – Lecture 5
- Nick Holliman – Formal Aspects Set Theory – Lecture 6
- Nick Holliman – Formal Aspects Set Theory – Lecture 7
- Discrete Mathematics and its Applications – Kenneth H Rosen – Sixth Edition